Řešení 3. série XVIII. ročníku

• 1. úloha

  Na nádraží stojí dvě vlakové soupravy s parními lokomotivami. První parní lokomotiva se jménem „Kafemlejnek“ má hmotnost 35 tun, druhá parní lokomotiva se jménem „Malý bejček“ má hmotnost 45 tun. První lokomotiva táhne 5 vagónů, druhá 8 vagónů. Každý vlak jede přes tři zastávky. Na první zastávce obě soupravy odpojí dva vagóny. Na druhé zastávce obě soupravy připojí 5 vagónů. Jenomže „Kafemlejnek“ se po připojení pěti vagónů na druhé zastávce porouchal. Naštěstí ho opravili, ale museli jeden vagón odpojit, aby to „Kafemlejnek“ uvezl. Na třetí zastávce obě soupravy dva vagóny odpojí.
  
  Kolik váží každá vlaková souprava při odjezdu ze třetí stanice, když víme, že jeden vagón má hmotnost 10 tun?
  
  

  ŘEŠENÍ

  
  První souprava = 85 tun (lokomotiva 35 t + vagóny 5 x 10 t) Druhá souprava = 135 tun (lokomotiva 45 t + vagóny 9 x 10 t)
  
  

• 2. úloha

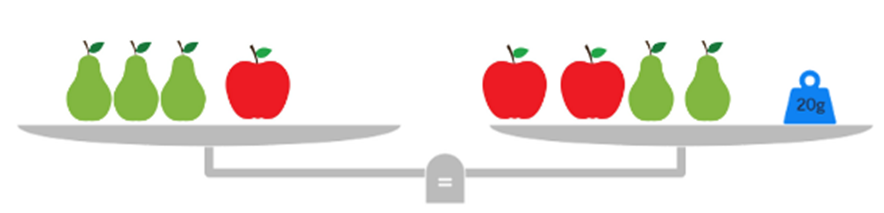
  Rovnoramenné váhy byly v rovnováze při zatížení, které znázorňuje obrázek:
  
  Dokážeš určit kdo kde žije a jakou má zálibu? Doplň tabulku.
  
  Všechny hrušky mají stejnou hmotnost, také všechna jablka mají stejnou hmotnost. Závaží má hmotnost 20 gramů. Určete hmotnost jedné hrušky, jestliže hmotnost všeho ovoce je 780 gramů.
  
  

  ŘEŠENÍ

  
  Odebereme-li z misek vah na každé straně 2 hrušky a jedno jablko, nalevo bude hruška a napravo jablko a 20 g závaží. Znamená to, že 1 hruška má o 20 g větší hmotnost než jablko. Tedy 5 hrušek má o 100 g větší hmotnost než 5 jablek. To znamená, že 5 hrušek a 3 jablka mají stejnou hmotnost jako 8 jablek a 100 g závaží. Všechno ovoce má 780 g. 8 jablek a 100 g musí mít také hmotnost 780 g. 8 jablek má hmotnost 680 g a 1 jablko tedy 85 g.
  
  Hruška váží 105 g. Řešit se dá také soustavou rovnic.
  
  

• 3. úloha

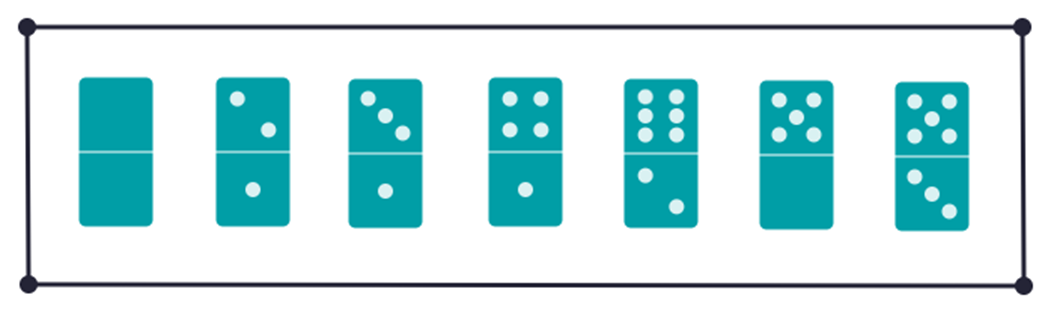
  Na obrázku je 7 kostek domina. Prvních šest vyhovují za sebou určité zákonitosti – pravidlu postupně v řadě, poslední sedmá kostka nevyhovuje pravidlu v této řadě. Jaká kostka nevyhovuje pravidlu? Jaké to pravidlo je?
  
  
  

  ŘEŠENÍ

  
  Rozdíl horního a dolního pole je postupně 0,1,2,…5
  u sedmé je rozdíl 2.
  
  

• 4. úloha

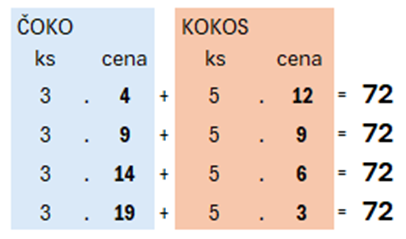
  Maminka zaplatila v obchodě za 3 čokoládové tyčky a 5 kokosových tyček dohromady 72 Kč.
  Kolik korun stála čokoládová a kolik korun kokosová tyčka, jestliže jejich ceny byly v celých korunách?
  
  Vypiš všechny možnosti řešení.
  
  
  

  ŘEŠENÍ

  
  
  
  

• 5. úloha

  Na přímé silnici jsou čtyři autobusové zastávky A,B, C, D.
  Nakreslete, jak jsou uspořádány, jestliže vzdálenost |AD| = 1 km, |BD| = 3 km, |AB| = 4 km, |CD| = 5 km.
  
  Určete vzdálenost zastávek A, C.
  Nápověda: zastávku A umístěte libovolně.
  Zakresli do obrázku, 1 dílek = 1 km.
  Prověř jestli existuje více variant rozmístění a zda existuje více možností vzdáleností zastávky A od C.
  
  
  
  

  ŘEŠENÍ

  
  Například
  
  Vzdálenost |AC| = 6 km
  
  

Řešení 4. série